기하학적 의미
수학의 기하학적인 의미는 시각적인 해석에 관한 이야기입니다. 매우 직관적이며 문제를 파악하기 위한 아주 중요한 표현방법입니다. 기하학을 이야기 하기 위해서는 중학교때 배우는 좌표에 관한 이야기를 먼저 해야 할거 같습니다. 좌표는 우리가 기하학을 언어적으로 해석할 때 가장 기본적인 표현방법이라고 생각합니다. 표현방법으로 사용하는 방식은 위치의 값을 수치로 표현하는 것입니다. 예를 들어 $(2,4)$, $(5,2)$, $(3,6,2)$ 등등 이러한 방식으로 사용할 수 있습니다.
여기서 중요한 것이 있습니다. 좌표는 모든사람이 공통으로 “0”을 기준으로 위치를 해석한다는 것입니다. 위치라는 것은 기준이라는 것이 존재해야만 어느 누가 해석을 하던 일정한 위치를 갖게 되는 것입니다. 우리가 배우는 좌표는 암묵적인 기준이 내포되어 있는 것입니다.
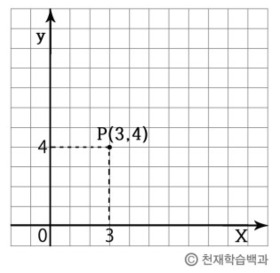
| 좌표의 여러가지 해석
좌표에 대한 표현 방식은 여러가지가 있습니다. 이 좌표를 대표하는 직각좌표계라는 것입니다. 위에서 언급했던 $(2,5)$식의 직각으로 이루어진 축에 대해서 값을 이용하여 위치를 표현하는 것입니다. 우리가 가장 많이 사용하는 좌표도 가장 먼저 배운 좌표입니다. 이외에도 극좌표계가 있습니다 극좌표계는 각과 거리를 이용하여 위치를 표현한 것입니다. 여기서 중요한 말은 “위치를 표현한다”는 것입니다. 이는 위치를 표현할 수 있는 방법은 여러가지고 있고 표현하는 방법에 따라 이름이 정해지는 것입니다. 예를 들어 원통좌표계, 구면좌표계, 천계 좌표계 등이 있습니다. 그러나 어려운 것은 없습니다. 핵심은 위치를 표현하는 방법의 차이라는 것입니다.
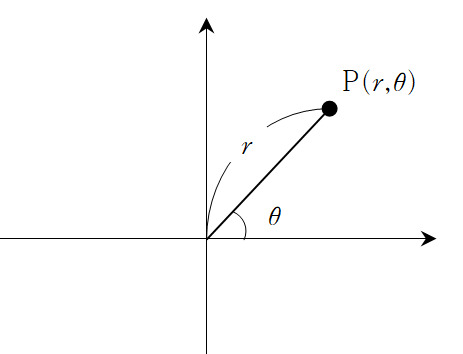 극좌표계
극좌표계
그래서 좌표의 해석은 표현하는 방법의 차이이며 이 차이를 이해하는 것이 중요한 것이라고 생각합니다. 이런 좌표를 표현하는 방식은 지극히 제한적입니다. 모든 좌표는 수와 각으로 이루어진다고 볼 수 있습니다. 자세하게 이야기 하면 수에서 실수와 허수를 이용한 표현과 각에서 시각적인 표현과 위도와 경도의 표현등 여러가지가 있을 것입니다. 하지만 크게 보면 수와 각을 이용하여 좌표를 표현합니다.
| 함수들의 계수들과 함수값들의 부호 파악
학생들을 가르칠 때 학생들이 함수에서 제일 이해를 못하던 부분 중 하나가 함수의 계수값과 함수값을 이용한 그래프의 위치를 파악하는 부분입니다. 계수나 함수값의 부호에 의해서 그래프의 모양이나 위치 등을 파악할 수 있는 이를 파악하는 부분을 학생들이 많이 어려워했습니다. 이 부분을 이해하기 좋은 방법은 계수값들에 의해서 그래프들이 어떻게 변화하는지 파악하는 것입니다. 그럼 먼저 일차함수를 이용해서 그래프의 변화를 보겠습니다.
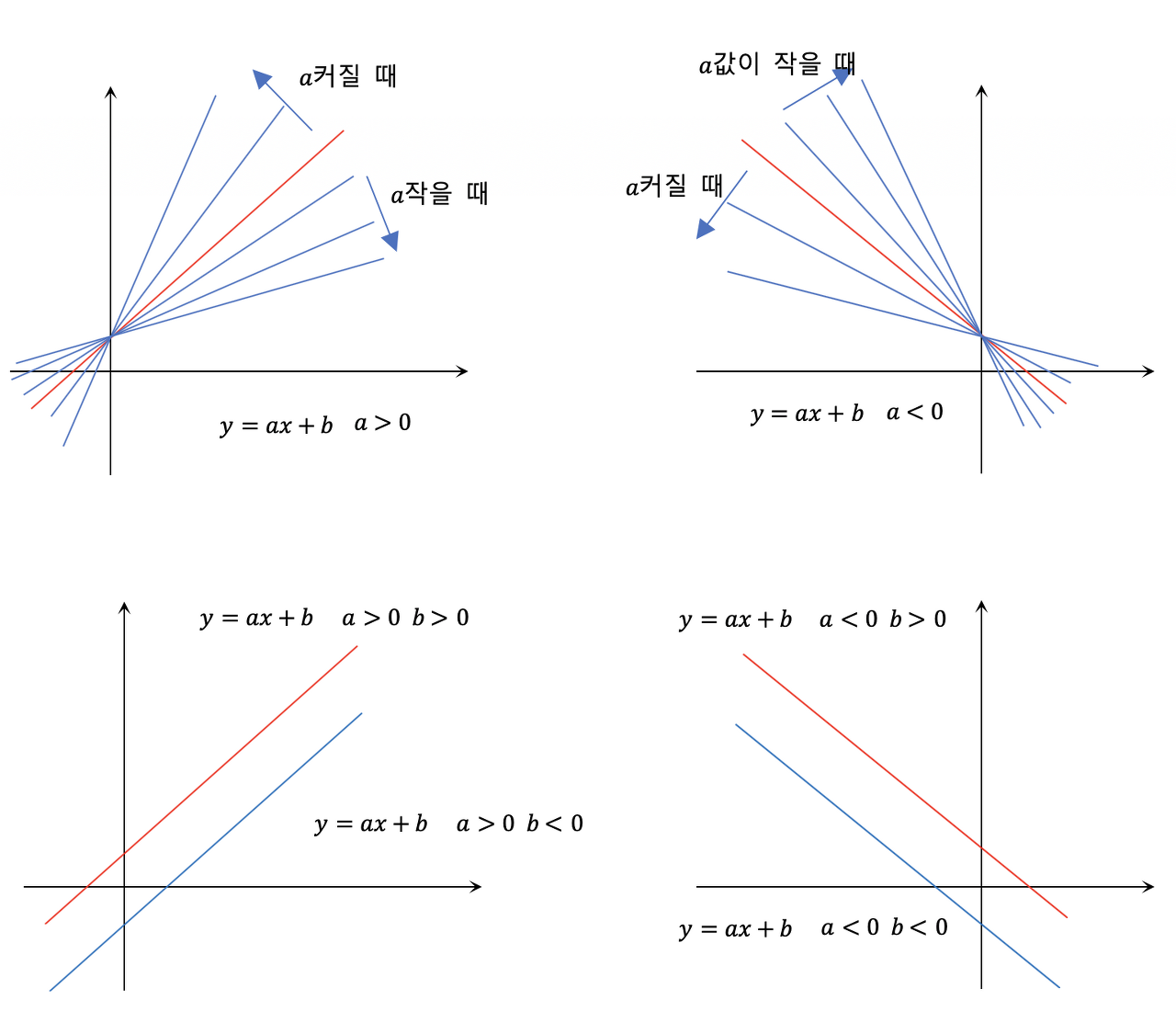
위의 그림과 같이 함수의 계수에 따라 그래프의 모양이 변화하는 것을 알 수 있습니다. 하지만 이부분을 외워야 하는 것은 아닙니다. 원리에 대한 이해가 중요합니다. 일차함수의 계수는 기울기와 $y$절편의 값으로 나누어 생각할 수 있습니다. 그래프의 기울기는 양수이면 증가하는 그래프의 모양을 갖고 음수이면 감소하는 그래프의 모양을 갖습니다. $y$절편은 그래프의 위치를 결정한다고 생각할 수 있습니다.
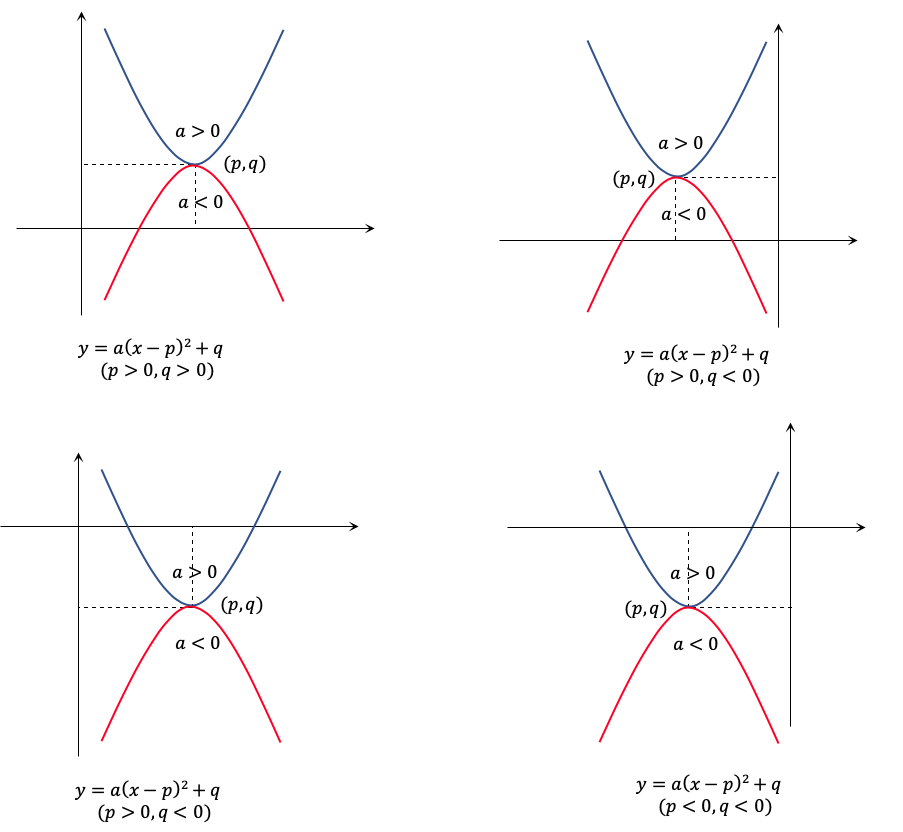
그럼 이제 이차함수로 확장을 해볼까요? 이차함수는 이차함수의 이동형 함수를 통해서 그래프의 계수값을 파악해 볼 수 있습니다.
이차함수의 이동형의 p, q의 값에 의해서 그래프의 위치가 변하는 것을 확인할 수 있고 a값에 의해서 아래로 볼록인지 위로 볼록인지를 확인할 수 있습니다.
이차함수의 일반형 $y=ax^2+bx+c$ 의 계수판단은 $a$는 앞의 내용과 같이 아래로 볼록인 위로 볼록인지를 파악할 수 있습니다. $c$는 절편의 위치를 판단합니다. 주어진 이차함수의 $x$값에 $x=0$을 대입하면 그래프이 위치를 파악할 수 있습니다.
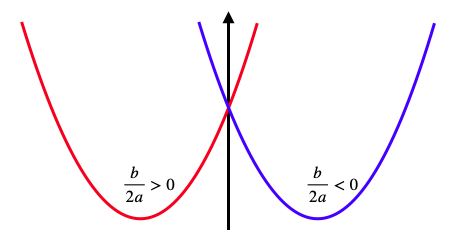
이제 잘 이해하지 못하는 부분은 $b$의 값의 판단입니다. $b$는 값을 판단하는 것이 아니라 부호를 판단하는 것입니다. 일반형을 완전제곱꼴의 형태로 변형하여 계수를 판단할 수 있습니다. 이차함의 완전제곱식은 $y=a(x+{\Large b \over \Large 2a})^2+c-{\Large b^2 \over \Large 2a}$입니다. 여기서 ${\Large b \over \Large 2a}$의 부호에 따라서 $x$축의 양의 방향으로 이동할 것인지 $x$축의 음의 방향으로 이동할 것인지 결정이 됩니다. 그럼 ${\Large b \over \Large 2a}>0$이 될려면 $a$와 $b$의 부호가 같아야 합니다. 또 ${\Large b \over \Large 2a}<0$이 될려면 $a$와 $b$의 부호가 달라야 합니다.
여기서 이야기하고 싶은 핵심은 수학적인 표현이나 설명이 아니라 계수들이 갖는 값이나 부호가 기하학적으로 의미를 갖고 있다는 것을 이해하는 것입니다. 만약 위의 내용을 이해하지 못하셨더라도 상관없습니다. 목적은 내용의 암기가 아닌 나중에 함수의 기하학적인 내용들에 대해서 찾아 볼 수 있는 것이 중요한 목적이라고 할 수 있습니다.

 오늘보다 나은 내일 위해 준비합니다.
오늘보다 나은 내일 위해 준비합니다.